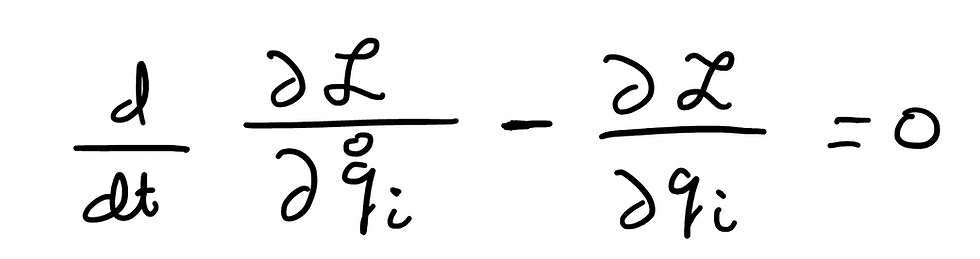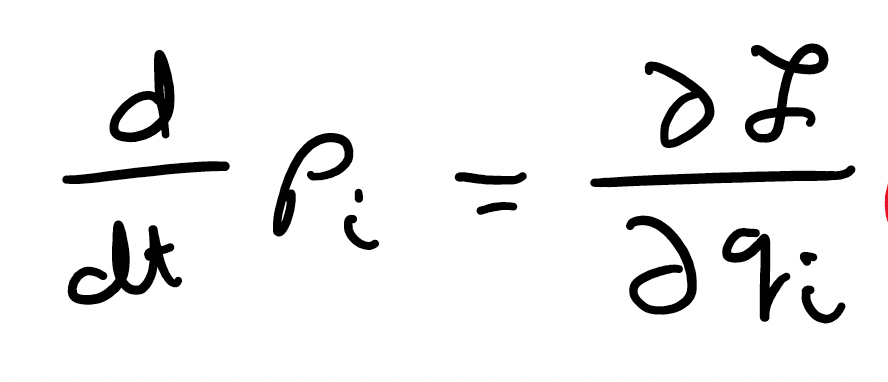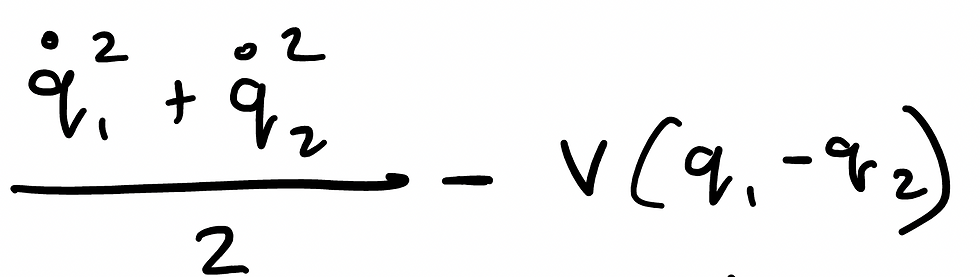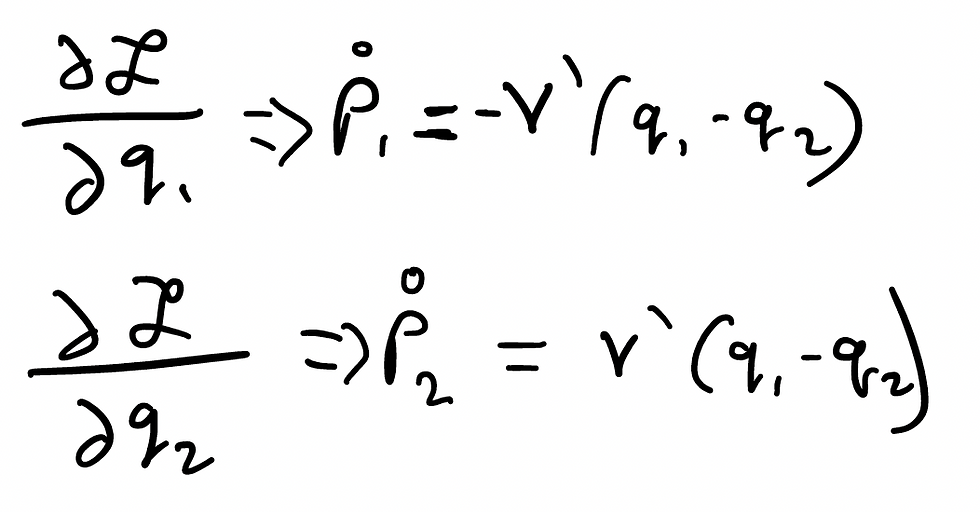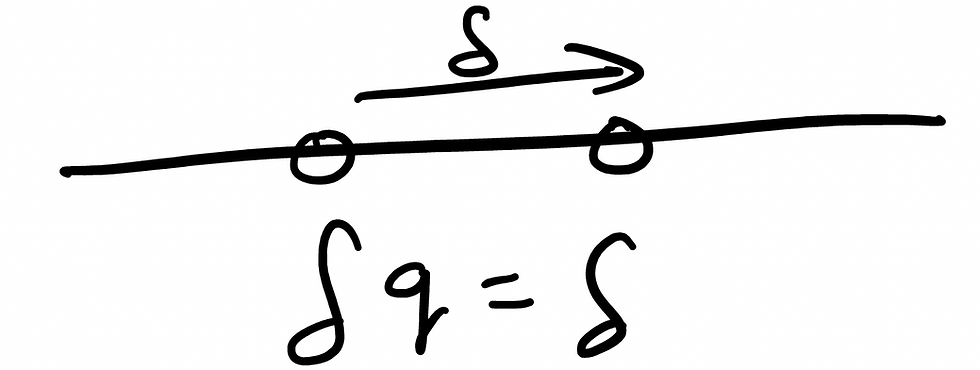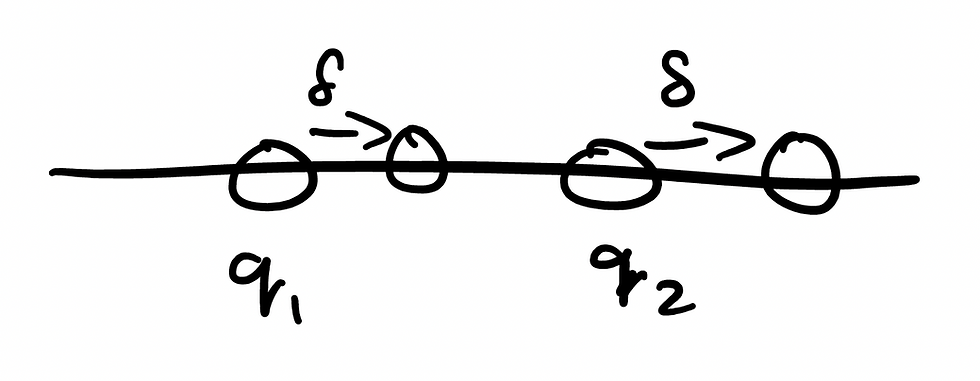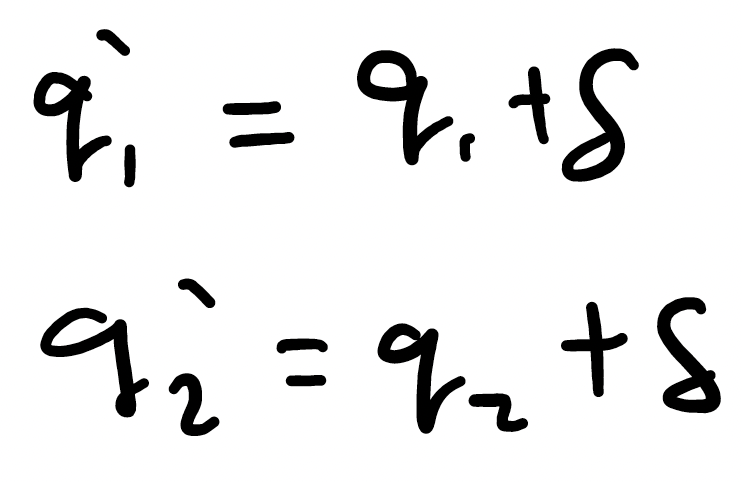Back to the (Quantum) basics

Hello, long time no see,

I am back after an extended, lazy sabbatical, and after a few years of putting this on the backburner, it's time to summon this page back to life.

I shall start with some basic notes on the basics of quantum physics, and try to make them even more basic than the basic notes themselves. Just like my coffee order, I will try and make it super basic (if that wasn't already clear).

I'm also keen on sharing some updates from arx.iv. That place is a godsend and I'd love to bring to light some of the newly released papers I find interesting on there.

Let's send this.

Symmetry & Conservation Laws (Part 2/2)

In my very very first post, I started giving a pseudo-scientific explanation for the origin of our universe. I say pseudo-scientific because everything I talked about -inflation and inflatons- is an active area of research in the field of cosmology. But, we are so far away from definitively proving the existence of inflatons that for now, the discussion is as good as science fiction.

What we do know about our universe for now is that we have many different galaxies. And within those galaxies we have stars and planets revolving in some systems.

Take our galaxy. Typical images of Milky Way show this cesspool of star and planetary systems converging towards a centre point, resembling a spiral devolving down into certain point. Similarly, all our galaxies are collectively also converging together in a similar spiral shape. Check the image above for a visualisation of what I'm talking about.

We talked in the last post about what symmetry and in particular translational and rotational symmetry meant. The main takeaway from that post was this: If, after a rotation or a translational, the potential energy in a system, and by extension the Lagrangian, does not change, then we have symmetry. And symmetry in turn implies a conserved quantity. In the case of rotational symmetry, we concluded that angular momentum is conserved.

Using this pretext, let's take the following system:

This shows a coordinate system with 3 different axis with a bunch of points. Now let's say that the entire system is rotating in the direction of the arrow shown. Note: it doesn't actually matter if you think of this as the points themselves moving or the entire coordinate system moving, the reasoning that follows applies for both scenarios.

Let's relate this situation to the takeaway we mentioned before. We have a rotation, and, if we know that potential energy does not change through this rotation, we know that angular momentum is conserved in this rotational symmetry. It doesn't matter how many points you have in this system, as long as they rotate together and the potential energy of the system does not change in this rotation, the total angular momentum is conserved.

If we apply this to a larger scale, we can use this methodology to conclude that if a planet is orbiting a star and its potential energy does not change, then its angular momentum is conserved.

This is really the culmination of our efforts through the past few posts in building up the Lagrangian, as I'm sure you can see how powerful a tool it is. Take away the coordinate points and place the Earth and other planets in our solar system into the system, with the sun as the centre and this gives you a powerful picture of our solar system.

All the planets orbiting around our central star, we can use this to calculate all of the preserved momentum present in these rotational cycles.

It's a powerful, powerful concept and one that required the series of posts that preceded it in order to fully appreciate the majesty of it. Astronomers and astrophysicists went crazy with this, and they still do.

Thank you to all those who followed along with the posts and diligently kept up with the immense pile of science I threw at you all. I'll be back soon with a topic even closer to me: quantum mechanics!

Symmetry & Conservation Laws (Part 1/2)

My last few posts have been less postings and more ramblings with way too much quant to entertain anyone. I acknowledge that, but trust me it's all fundamental and necessary building blocks for what I'm about to discuss. This post has less math, or rather the math that I will discuss isn't necessary to understand in order to get what the post is about.

Conservation, or conserving something, can be defined as keeping something in a constant state. If you conserve a piece of artefact from Ancient Greece, it really means that there aren't any hooligans scribbling graffiti over a rosetta stone. Bloody teenagers.

Conservation has the same meaning in physics. If I say that a quantity is conserved, it really means that there is no loss or gain of that particular quantity. If I say that energy in a system is conserved, it really means that I'm not losing any energy, and hence not gaining any, in this system.

Got it? Good. The next thing we need to define is symmetry. In our ordinary lives, symmetry is often described as two sides of a system which are equivalent. In physics, symmetry takes on a slightly different meaning. The simplest definition of symmetry is when an object/particle is placed at a different set of coordinates than where ti originates and the Lagrangian (kinetic - potential) remains the same. It essentially means that the Lagrangian is the same no matter where the particle is located within the system.

Now that we have defined these things, let me tell you that the next few lines are going to be mathematical - filled with equations and formulas and also using a lot of what I've derived in the last few posts.

So previously we defined a principle of stationary action, or the Euler Lagrange Equation (E-L-E). Let's define that again: (If you've forgotten or interested in how this was derived, check out my last post)

Note: following the notation used by classical mechanical framework, I am replacing x with q. Don't ask me why, blame Lagrange.

Before we move ahead, we are going to specify a new definition. The left hand side, specifying the time derivative term, is known as the momentum conjugate and is defined as such:

It's actually called the canonical momentum and is defined as such by Wikipedia:

In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time

So, this term essentially allows us to measure the momentum of a particle at any set of coordinates in a system. We can now rewrite this equality so that:

Since the last few posts saw me defining these equations and not actually doing any math, on popular demand, let's look at an example system and how exactly we would solve problems using this.

The Example:

I'm going to define the Lagrangian as:

q1 and q2 are essentially two coordinate of particles. The left term in this is the kinetic energy and the right term is the potential energy. We assume the mass to be 1 so the derivation of the KE makes sense. PE is interesting - note that it's dependant on separation of the particles, not on the positions of the particles themselves. Let's derive the canonical momentums:

If we take the next step and plug this into the E-L-E, we get the following:

And if you've read the conclusion of my previous post, you'll know that this signifies a conservation law. Neat, right? And what is conserved? Well, its momentum! Or rather, a function of the momentums of both the particles. That's pretty clear from our derivation.

Returning to the topic of symmetry:

So now that we've established how we are to use the E-L-E to find conserved quantities, let's return back to the topic of symmetry. We are again going to do some math, so bear with me here. Imagine a particle existing on a straight line:

It's a pretty crude drawing but I trust all of you to use your imaginations. We can say that this particle is currently at position q. Now, what if we shift this particle along this line? Say by a quantity delta?

Let me ask you this, what do you think happens to velocity? On first instance you might say that it changes because the position of the particle changes. But velocity is comprised of speed and direction, not position at all! So the fact that we have a new quantity which is a constant more than the previous quantity, this new position has absolutely no change on the velocity of the particle.

And, and this is key, if the velocity doesn't change, then the Lagrangian does not change at all. Look back on my previous post, you'll see that there isn't a term in the Lagrangian for the position (q) but only for the velocity. So, if velocity remains constant, the Lagrangian remains constant.

And, and and, since the Lagrangian hasn't changed, but the position of the particle within the system has changed, this proves to be an example of symmetry! In particular, this movement is what we call translational symmetry since we are translating space essentially.

Just to drill this point in, let's take another example. Instead of one, let's now consider two particles in the same phase space:

Let's define the transformations that took place:

And since the positions of both particles are changed only by a constant, this does not change the potential and kinetic energies and therefore, does not change the Lagrangian. So, we have another example of translational symmetry. But, there's also a hidden sort of derivation that we've made through this calculation. When we say that the velocity of both these particles are not changing, and the kinetic and potential energies are not changing, we also mean that the canonical momentum of both these particles aren't changing. What does this mean? Well simply that the time derivatives of the canonical momentums is 0.

Conservation Law! That's the first thing that might have popped into your head, and if it is, then you are correct! In fact, this brings us to the first important conclusion of this post:

If there is translational symmetry, the momentum of the particle is conserved.

Let's take a more complex example now:

Remember how we worked an example in an earlier post with a rotating coordinate frame? Well that was warm-up for what we are doing here. Let's take a normal cartesian x,y coordinate plane. And let's fiddle with it: rotate it by an angle theta:

So we are essentially rotating the coordinate frame. We'll define the Lagrangian as such:

Note: PE is dependant on the distance of the particle from the origin.

And since we have two different coordinate frame, it's important for us to define the new coordinate systems using the old as a reference frame. We do the following:

What I'm going to do now is prove that this rotating piece of mess is actually symmetric. Let's take an extremely small theta which gives us the following quantities:

If we replace some quantities from our previous equations, we get the following simplified notions:

And so:

Now let's check that the Lagrangian does not change step-by-step:

First let's check that PE does not change:

Therefore:

Similarly, if we try to find the same derivations for KE, we get:

And so, KE is constant as well.

Since neither KE or PE change, the Lagrangian remains constant.

And so we have proven symmetry for a rotational translation as well. But it's not exactly clear what (if anything) is being conserved in this. It's all just a bit too complex. So let's take a more general approach and see what that gives us.

If we look above, what we see is that any type of movement, rotational or translation, and we can generalise this movement using the following equation:

The movement is essentially the constant multiplied by some function of position. Note the i represents different particles. And so we can also define:

Using this, what we want to find is the conserved quantities, something which wasn't clear earlier. The next few mathematics are a series of calculations I have conducted in order to derive the conserved quantity. I am attaching my notes here. Anyone interested can refer to the full calculations in this:

Lecture 4- conservation laws and symmetry.pdf

Download PDF • 70.60MB

For the sake of time and to save you all from boredom, I'll skip right to the point.

Using these initial derivations, we get the following:

Q stands for the conserved quantity. Thus, we have derived a formula for calculating which quantities are preserved in a given system. I encourage you all to look through my notes and see how this was calculated - it's a fascinating process with some very important assumptions.

Using only the assumption of symmetry, we can now find which quantities are conserved in a system.

Let's see this in action:

First taking the example of a system with translational symmetry, we found the following:

Comparing this to the above formula, we can specify:

And so, the summation gives us:

THIS is the quantity that is preserved. The momentum is conserved. And as we mentioned before, this is true for any translational symmetry systems.

Now let's take an example of a system with rotational symmetry:

This is just what we calculated earlier. The summation now becomes:

And since in a rotationally symmetric setting x and y represents the angles that make up the rotating coordinate frame, the quantity that is conserved is the Angular Momentum. Angular momentum is essentially the same thing as momentum but for an object that is rotating.

SO, let's take a breath. That's a whole lot of information in one post. I'm gonna put a handy summary here for people for whom it might just be TL;DR.

Summary:

1. If there is translational symmetry, momentum is conserved

2. If there is rotational symmetry, angular momentum is conserved

3. We can find symmetries by comparing if the Lagrangian has changed when the particle changes positions

Some may be thinking, what about energy? Well, energy conservation is the one thing we haven't actually talked about. We'll get there. Many people use Hamiltonian mechanics to describe this but I like to use quantum mechanics. There's still some time to get there.

In the continuation of this post, I will talk about how 1 particular conclusion from these results (conservation of angular momentum) explain why our universe is the way it is. Sounds complex, but we'll go through it together.

See you all soon!!