Symmetry & Conservation Laws (Part 2/2)
- Adi Thakur
- Aug 30, 2021
- 3 min read

In my very very first post, I started giving a pseudo-scientific explanation for the origin of our universe. I say pseudo-scientific because everything I talked about -inflation and inflatons- is an active area of research in the field of cosmology. But, we are so far away from definitively proving the existence of inflatons that for now, the discussion is as good as science fiction.
What we do know about our universe for now is that we have many different galaxies. And within those galaxies we have stars and planets revolving in some systems.
Take our galaxy. Typical images of Milky Way show this cesspool of star and planetary systems converging towards a centre point, resembling a spiral devolving down into certain point. Similarly, all our galaxies are collectively also converging together in a similar spiral shape. Check the image above for a visualisation of what I'm talking about.
We talked in the last post about what symmetry and in particular translational and rotational symmetry meant. The main takeaway from that post was this: If, after a rotation or a translational, the potential energy in a system, and by extension the Lagrangian, does not change, then we have symmetry. And symmetry in turn implies a conserved quantity. In the case of rotational symmetry, we concluded that angular momentum is conserved.
Using this pretext, let's take the following system:
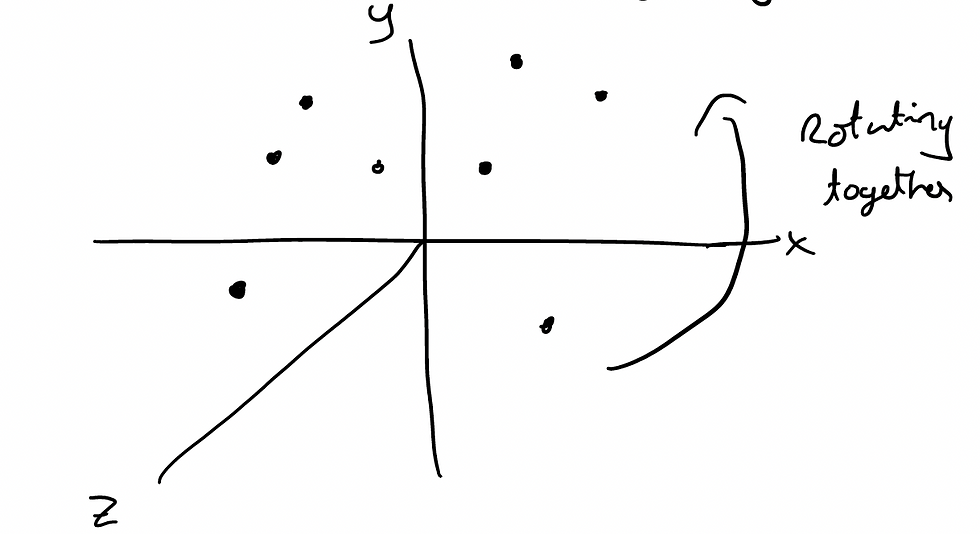
This shows a coordinate system with 3 different axis with a bunch of points. Now let's say that the entire system is rotating in the direction of the arrow shown. Note: it doesn't actually matter if you think of this as the points themselves moving or the entire coordinate system moving, the reasoning that follows applies for both scenarios.
Let's relate this situation to the takeaway we mentioned before. We have a rotation, and, if we know that potential energy does not change through this rotation, we know that angular momentum is conserved in this rotational symmetry. It doesn't matter how many points you have in this system, as long as they rotate together and the potential energy of the system does not change in this rotation, the total angular momentum is conserved.
If we apply this to a larger scale, we can use this methodology to conclude that if a planet is orbiting a star and its potential energy does not change, then its angular momentum is conserved.
This is really the culmination of our efforts through the past few posts in building up the Lagrangian, as I'm sure you can see how powerful a tool it is. Take away the coordinate points and place the Earth and other planets in our solar system into the system, with the sun as the centre and this gives you a powerful picture of our solar system.
All the planets orbiting around our central star, we can use this to calculate all of the preserved momentum present in these rotational cycles.
It's a powerful, powerful concept and one that required the series of posts that preceded it in order to fully appreciate the majesty of it. Astronomers and astrophysicists went crazy with this, and they still do.
Thank you to all those who followed along with the posts and diligently kept up with the immense pile of science I threw at you all. I'll be back soon with a topic even closer to me: quantum mechanics!

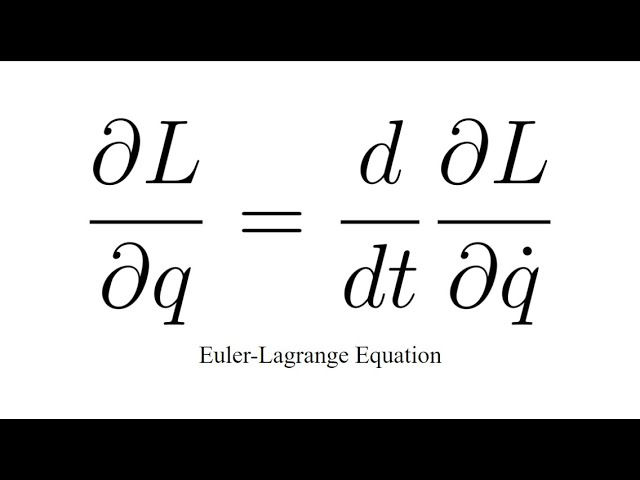
Comments