Euler-Lagrange Equation - why is it so useful? (Part 2/2)

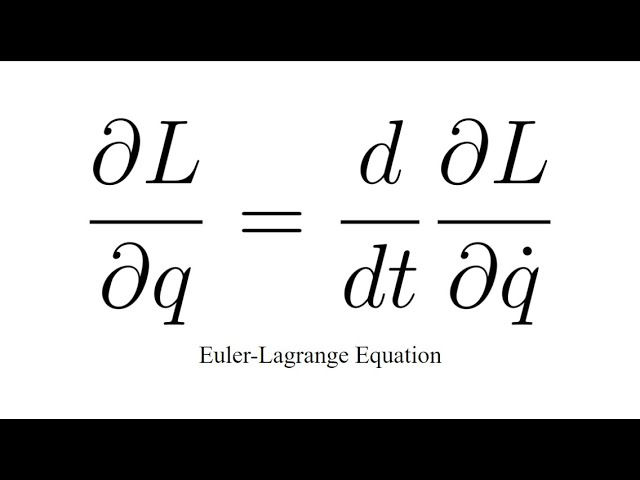
In my last post I mentioned two main advantages of this equation in the world of physics and particularly the modelling of the law of motion. In this post, I'm going to delve a bit deeper on both these advantages. And for those of you who think I've gone crazy about this one particular mathematical equation, don't worry! I have something in store for all of you in the next post (hint: everything we are doing here can be used to calculate stuff about the orbit of the Earth, our solar system, our galaxy and really our whole universe). So yeah, pretty important stuff here.

Let's dive in:

1. Its form is essentially the same in any coordinate system. This means you can switch between cartesian, polar and other coordinate systems with multiple variables seamlessly using this equation. Trying to apply Newtonian equations in these different systems would be tedious without this 'translator'. In particular, this equation implicitly encompasses the basic laws of physics.

So, this is probably the hardest to prove. But here's my attempt at it.

Let's prove this by looking at a conversion between two coordinate systems that most of you have probable heard of: cartesian and polar. For those of you who may need a refresher, the cartesian coordinate system is our usual x-y coordinates. The polar system defines coordinates by taking their distance from the origin and the angle made by this point. Here's a simple polar coordinate system:

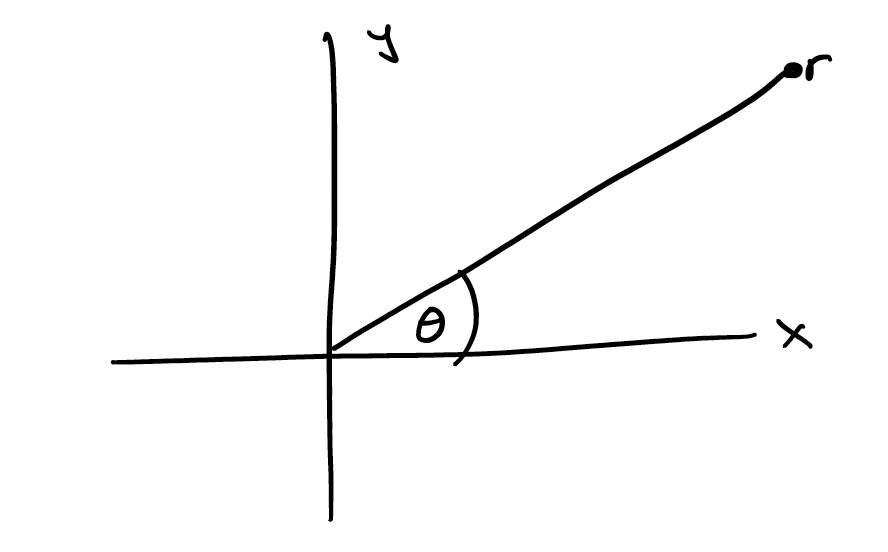
Theta represents the angle that we measure. Coordinates in this system are derived using the following equalities:

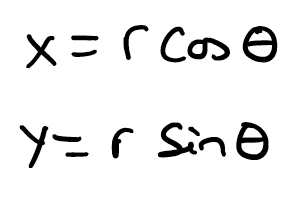
Now, let's define our Lagrangian as the Kinetic Energy (KE) minus the Potential Energy (PE). This is quite conventional, as this represents the total energy existing in a system (remember that total energy consists of both kinetic and potential energy). Let's define our Lagrangian in such a manner:

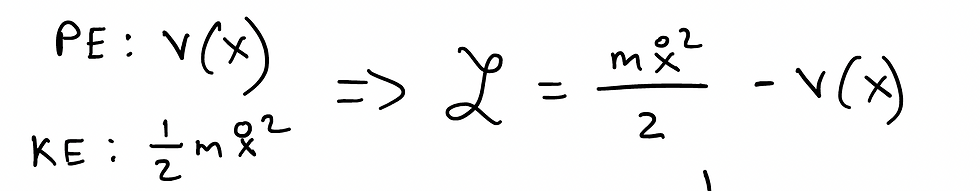
In this, V(X) represents the potential energy and the second formula is for the kinetic energy. From elementary physics, we know the formula of KE to be 1/2*mv^2 where m stands for mass and v stands for velocity. Anyone who has read my notes on introductory cosmology will know that an open circle over a variable represents the time derivative of that variable. Since x has represented position in my notes, an open circle over x is the time derivative of position, which is velocity. Both these energies make up our Lagrangian.

Let's adapt this a little bit to fit our polar coordinate plane. The PE will remain the same, except instead of having x as the position of our particle, we now have r. This is because the radius represents the position of a particle as it makes its way through the system in a polar plane (it's one of the underlying mechanisms of a polar coordinate system). The KE will change a bit. The velocity is now dependant on both x and y, since they both represent the position of the particle, which in turn impacts the velocities. So our velocity is now a sum of our individual time derivatives of x and y. As such, our kinetic energy formula can be defined as:

And replacing the x and y with our polar equivalents, we get the following result for our Lagrangian:

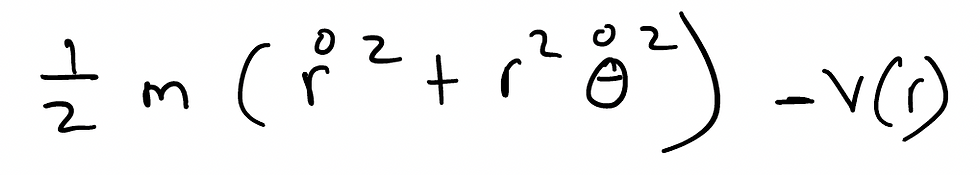
We've got our Lagrangian and we're now ready to go. Let's revisit the Euler-Lagrange Equation (E-L-E):

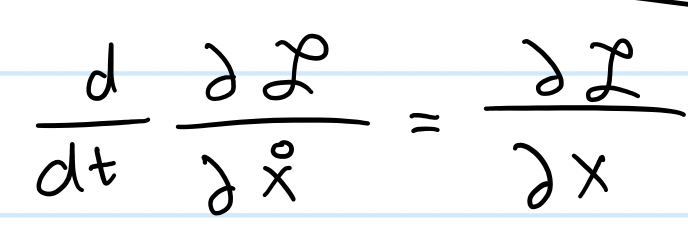
I'm going to focus on the left-hand side first. It tells me that I should first take a partial derivative of the Lagrangian with respect to the velocity.

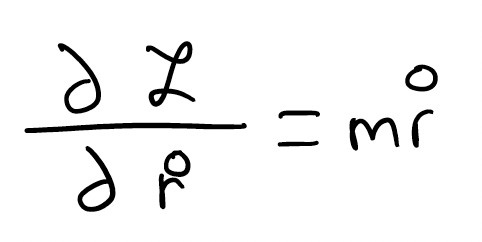
Next, I'm going to differentiate this with respect to time:

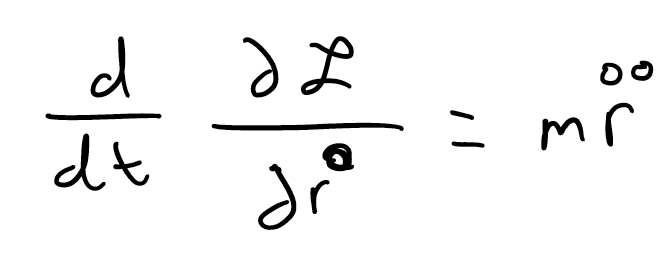
I'm now going to equate this to the right hand side of the ELE. The RHS dictates that I take a partial derivative of the Lagrangian with respect to the position and by doing so, I get:

And so, the answer to this is as simple as solving a differential equation. Using its solution, you would be able to solve problems within the laws of motion and physics. In such a way, the ELE can help converting between coordinate systems quite simply. We replaced the x-y cartesian coordinates with their polar counterparts. This might seem a bit complex, and that's because it is. It's not simple mathematics and I've presented a rather rudimentary version of a coordinate change using the powerful equation that we derived in the previous post. I'll link some videos and books that I believe describe this equation in greater detail. But for now, I'll move on to the next point.

2. A fascinating solution to a part of this equation can reveal whether there is a conservation law.

Let's pick up where we left off in the previous section. We are now going to explore the characteristics of theta. And to find these, instead of taking the partial derivative of the Lagrangian with respect to velocity, let's take it with respect to theta. Doing this, we get a peculiar solution:

Look familiar? Don't worry if it doesn't, it's the formula for angular momentum. And one trait of angular momentum is that it does not change along with time, in that it's not directly affected by time as a variable. So following the LHS of the ELE, we get:

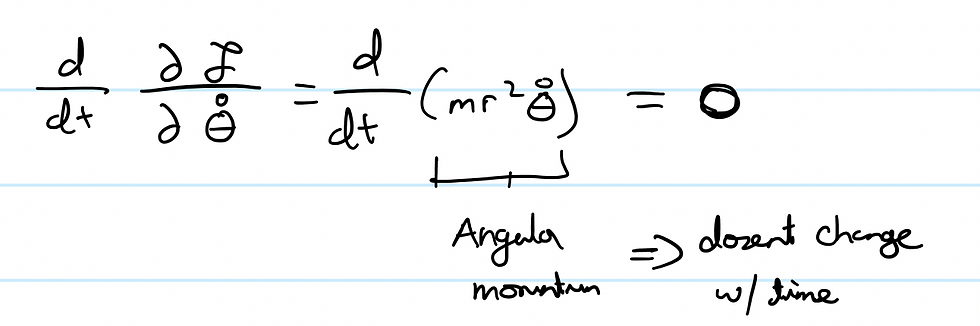
And so, we have successfully uncovered a fascinating result. If we take the time derivative of the partial of a Lagrangian, and the result is zero, we can say that the quantity is conserved. In this scenario, we say that the angular momentum is conserved.

In general, if a Lagrangian does not have a particular coordinate (in this case, it wasn't dependant on time) then the time derivative of it will be equal to 0 and we can identify it as a conservation law.

And in such a manner, we've proven two important characteristics of the ELE. While the first is insanely useful which conducting any activity in classical physics, I cannot stress how impactful the second application of the ELE is. In fact, in my next post, I'm going to compile all this information into a general, non-mathematical context and talk about what exactly does all of this imply in our world - the real world. And trust me, it implies a lot.

Till then, take some time to digest this information. I'm not an expert on any of this but rather just a student. It took me quite some time to wrap my head around many aspects of these applications of the ELE and if it's the same for you definitely reach out and I'll try and explain it in a simpler manner. See you soon!